Generalized Constraint Satisfaction

This project is one I enjoyed working on quite a bit, as it came from a school project and developed into something more involved. The goal was to create a program that could find values for variables that fit every rule/constraint given. The constraints were nonlinear, and were basically numerical versions of Einstein's Zebra Puzzle.

Example Constraints

The constraints would be something like:

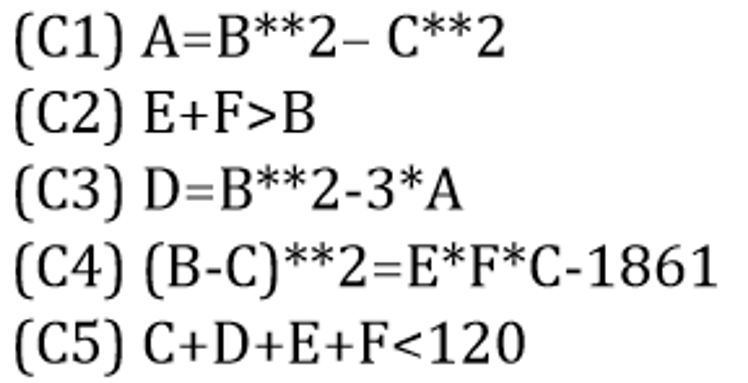
Example of constraint equations

The program would determine values for A, B, C, D, E, and F. In this case, they are:

A = 15
B = 8
C = 7
D = 19
E = 7
F = 38

This was determined in 1,940 total variable assignments. Brute forcing would have taken around 160,000,000 variable assignments (to reach this solution). This program can handle 26 variables and basically an unlimited number of constraints (more than 30 constraints realistically does not restrict the domain any further).

Algorithm

The program uses a combination of recursive backtracking, domain pruning, and forward thinking to reduce the number of variable assignments so drastically. The most notable of which is the domain pruning, where we look ahead at all possible values for a variable, and sort them according to their "expected restrictedness". For example, if one constraint is A = 3 * B, we would remove all values greater than [some value] from B's domain (We use [some value] here because the max value per variable can be modified). In the program, we look 2 levels ahead, removing values from one variable's domain that soon cause a constraint violation.

Customization

Nothing in this program is hard coded, so you can add any constraints you want, any number of variables, and a valid solution will be found in a decent amount of time. To add your own constraint, use this format:

(lambda x: x['A'] == x['B']**2 - x['C']**2, ['A', 'B', 'C'])

The x['letter'] just allows that variable to be referenced in this line, and the array of characters at the end is just an easy way to see which variables are concerned with this formula. (We would ignore any checking of the variable D to see if this constraint is valid, for example)

Main Function

Most of the customization that can be done is in the main function:

def main():
    Vrange = (1,120)
    variables = ['A', 'B', 'C', 'D', 'E', 'F', 'G', 'H', 'I', 'J', 'K', 'L', 'M']
    constraints = [
        #(lambda x: x['A'] > x['B'] + x['C'], ['A', 'B', 'C']),
        (lambda x: x['A'] == x['B']**2 - x['C']**2, ['A', 'B', 'C']),
        (lambda x: x['E'] + x['F'] > x['B'], ['E', 'F', 'B']),
        (lambda x: x['D'] == x['B']**2 - 3 * x['A'], ['D', 'B', 'A']),
        (lambda x: (x['B'] - x['C']) ** 2 == x['E'] * x['F'] * x['C'] - 1861, ['B', 'C', 'E', 'F']),
        (lambda x: x['C'] + x['D'] + x['E'] + x['F'] < 120, ['C', 'D', 'E', 'F']),
        # Problem B constraints
        (lambda x: (x['G'] + x['I'])**3 == (x['H'] - x['A'] - 1)**2, ['G', 'I', 'H', 'A']),
        (lambda x: x['B'] * x['E'] * x['F'] == x['H'] * x['B'] - 200, ['B', 'E', 'F', 'H']),
        (lambda x: (x['C'] + x['I'])**2 == x['B'] * x['E'] * (x['G'] + 1), ['C', 'I', 'B', 'E', 'G']),
        (lambda x: x['G'] + x['I'] < x['E'], ['G', 'I', 'E']),
        (lambda x: x['D'] + x['H'] > 180, ['D', 'H']),
        (lambda x: x['J'] < x['H'] - x['C'] - x['G'], ['J', 'H', 'C', 'G']),
        (lambda x: x['J'] > x['B'] * x['G'] + x['D'] + x['E'] + x['G'], ['J', 'B', 'G', 'D', 'E']),
        # Problem C constraints
        (lambda x: x['K'] * x['L'] * x['M'] == x['B'] * (x['B'] + 5), ['K', 'L', 'M', 'B']),
        (lambda x: x['F']**3 == x['K']**2 * x['M']**2 * 10 + 331, ['F', 'K', 'M']),
        (lambda x: x['H'] * x['M']**2 == x['J'] * x['K'] - 20, ['H', 'M', 'J', 'K']),
        (lambda x: x['J'] + x['L'] == x['I'] * x['L'], ['J', 'L', 'I']),
        (lambda x: x['A'] + x['D'] + x['M'] == x['B'] * (x['F'] - 2), ['A', 'D', 'M', 'B', 'F'])
    ]
    numConstraints = 17  # Number of constraints to actually use
    numVariables = 13    # Number of variables to actually use
    nva = [0]  # Number of variable assignments tracker

    domains = {var: list(range(Vrange[0], Vrange[1]+1)) for var in variables}
    assignment = {}
    print("number of constraints:", numConstraints)
    print("selected variables: ", variables[:numVariables])

    # find one solution for the given inputs
    solution = recursiveBacktracking(
        assignment, 
        variables[:numVariables], 
        domains, 
        constraints[:numConstraints], 
        nva
    )